How does a Genetic Algorithm work?

Genetic Algorithms are a subset of Evolutionary Algorithms, a group of search and optimisation engines inspired by the natural process of evolution. Evolutionary Algorithms typically use evolutionary selection, variation, and replacement operations to augment or replace populations in a generational manner in order to improve the overall fittest solution. An example of this process cycle is shown in Fig. 1.

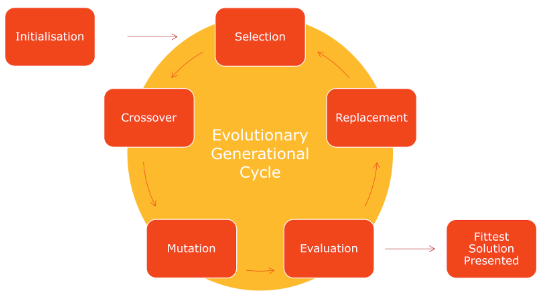
Figure 1: The evolutionary cycle of a typical evolutionary algorithm. Each block represents an operation on a population of candidate solutions.

Initialization

The evolutionary process begins with initialization, wherein an initial population of candidate solutions is generated. There are many different methods of initializing populations, but with Genetic Algorithms the most popular method of initialization is simply to create a population of randomly initialized binary strings. Once the initial population has been created, the evolutionary generational cycle begins.

Selection

At each generational step, a pool of parents is chosen from the parent population based on the fitness values of each individual using a selection mechanism, such that the fittest individuals will have a greater probability of passing on genetic material to subsequent generations. This selected population (known as the “parent” population) then forms the basis for all subsequent optimizations during the generational step.

Variation

Once the parent population is fully populated via the selection process, a child population is created which will form the basis of the next generation. This child population is generated by variation operators, which are performed on individuals from the parent population. The most prominent such methods are crossover and mutation.

Crossover

Crossover takes pairs of parents from the parent population (usually random selection with replacement, such that the same parent can be selected multiple times to produce children). These parents then have some of their genetic information swapped between them. Crossover of two parent chromosomes is usually done in a single-point manner, where a single crossover point on both chromosomes is randomly selected and then all subsequent genetic information is swapped between individuals, as shown in Fig. 2:

Figure 2: Single-point crossover of two parent GA chromosomes

Crossover is typically performed on randomly selected pairs of parents from the parent population until the new “child” population reaches the same size as the original parent population.

Mutation

While crossover simply swaps pre-existing information between pairs of candidate solutions, mutation in Evolutionary Algorithms is typically the standard method of introducing “new” genetic material into the population. Once the child population has been created via crossover, mutation in canonical Genetic Algorithms then occurs on all children in a “bit-flip” fashion by randomly changing codons on the chromosome between 0 and 1 (as shown in Fig. 3).

Figure 3: Bit-flip mutation of GA chromosome

Evaluation

Once the child population has been created, all children then need to be evaluated in order to assign a fitness value by which they can be judged against their peers. This fitness is used to sort/rank a population and to impose probabilities for both selection and replacement phases of the search process, such that the fittest members of the population have a higher probability of passing on genetic material.

Replacement

The final act of the generational step is to replace the old “N” population with the new “N+1” child population. While many methods exist, the most typical replacement method is Generational Replacement, wherein the entire previous generation is replaced with the newly generated child population.

Termination

A Genetic Algorithm will typically terminate after a predefined number of generations, or if some stopping criterion has been met (e.g. fitness is above some threshold, error rate is below some threshold, etc). The fittest solution in the population is then returned as the overall best solution.